3次元点集合データ(ポイントクラウド)の解析¶
この文章で解説するのは
- 3次元の点データからパーシステント図を計算する
- その図をパラメータを変えながら可視化する
- 各birth/death timeを抽出する
- 逆解析を行う
の4つです。ここまではおよそどのようなポイントクラウドデータでも 共通ですので、ここまでできるようになると良いでしょう。
import homcloud.interface as hc # HomCloudのインターフェース
import numpy as np # NumPy (数値配列)
import matplotlib.pyplot as plt # Matplotlib (PDの可視化用)
%matplotlib inline
import pyvista as pv # PyVista (3D可視化)
3次元可視化のバックエンドを trame にします (see https://docs.pyvista.org/user-guide/jupyter/index.html )．
3次元可視化がうまく動かないときは'trame'を'panel'に変更してみてください．
pv.set_jupyter_backend('trame')
データを np.loadtxt で読みこみます。
pointcloud = np.loadtxt("pointcloud.txt")
まずは pointcloud の情報を調べてみましょう．
pointcloud.shape
(1000, 3)
np.min(pointcloud, axis=0), np.max(pointcloud, axis=0)
(array([0.00026274, 0.00100671, 0.00020878]), array([0.99997803, 0.9993682 , 0.99825316]))
データは 1000x3 の配列です．これは3次元の点が1000個あることを意味します． またX，Y，Z座標の最大最小を見るとデータは$[0, 1]\times[0, 1]\times[0, 1]$という立方体に分布していることがわかります． この点を可視化してみます．
plotter = pv.Plotter()
plotter.add_mesh(pv.PointSet(pointcloud))
plotter.show()
Widget(value="<iframe src='http://localhost:35823/index.html?ui=P_0x7f948df3c670_0&reconnect=auto' style='widt…
次のように可視化されます．
データからパーシステント図を計算します。hc.PDList.from_alpha_filtrationという静的メソッドを使います。
save_boundary_map は後で optimal volume というものを計算するのに必要です。
hc.PDList.from_alpha_filtration(pointcloud,
save_to="pointcloud.pdgm",
save_boundary_map=True)
PDList(path=pointcloud.pdgm)
すると pointcloud.pdgm というファイルが生成されます。これが
パーシステント図の情報を収めたファイルです。
pdlist = hc.PDList("pointcloud.pdgm")
このオブジェクトはすべての次数のパーシステント図を保持している(0次から2次まで)ので、1次のパーシステント図だけ取り出します。
すべての次数を保持しているので、このクラス自体の名前はPDListという名前です。
pd1 = pdlist.dth_diagram(1)
このメソッドの返り値は PD class のインスタンスです。
ヒストグラムを構築し、パーシステント図をプロットします。
histogramメソッドでヒストグラムを構築し、plotでそれをプロットします。
pd1.histogram().plot()
左下のほうに何かちょっと見えてあとはかなりぼんやりしています。というのは このデータは左下のほうにデータ(birth-death pair)が偏っているからです。 そこで色付けを log scale にしましょう。
pd1.histogram().plot(colorbar={"type": "log"})
基本的にはパーシステント図の点は対角線から離れるほど「意味のある」リング構造と対応し、 またY軸が大きい値になるほど大きなリング構造を表しています。 つまり(0.0025, 0.008)のあたりにある点がリング構造のなかで最もちゃんとしたリング構造を持っているものと対応していると言えそうです。
ここで注意しておくと、パーシステント図のX、Y軸は点に貼り付ける球の半径と対応していると
よくある教科書には書かれています。HomCloudでは実はこれは半径の2乗が使われています。
つまり$\sqrt{0.0025}=0.5$と$\sqrt{0.008} \approx 0.09$
が実際の半径になります。これは主には内部のアルゴリズムの都合に
よるものですが、各点に重みづけをしたときにはこのほうが自然に見えるという事情もあり、
HomCloudでは2乗の値が使われます。これを止めたいときはパーシステント図をhc.PDList.from_alpha_filtration
で計算するときに no_squared=True という引数を付けると
半径パラメータそのものがX、Y軸に現れます。
さて、次にbirth-death pairが集中している
左下の 0.0〜0.01 のあたりを拡大して調べてみましょう。デフォルトでは
ヒストグラムを構築するときにすべてのbirth-death pairが含まれるような
範囲を自動的に切り取ります。これを変更するには histogram メソッドのx_range引数（第1引数）を指定します。
pd1.histogram((0, 0.01)).plot(colorbar={"type": "log"})
ヒストグラムの解像度を変更するには histogram メソッドの
x_bins引数（第2引数）を指定します。デフォルトでは
128x128でヒストグラムを描きますが、もっと細かく256x256にしてみましょう。
pd1.histogram((0, 0.01), 256).plot(colorbar={"type": "log"})
これらの図は matplotlib の機能を使って描画されているため、
matplotlib.pyplot.savefigで保存することができます。以下のようにすると、pointcloud-pd1.pngに図が保存されます。
pd1.histogram((0, 0.01), 256).plot(colorbar={"type": "log"})
plt.savefig("pointcloud-pd1.png")
2次元のPDも同様に可視化しましょう．
pd2 = pdlist.dth_diagram(2)
pd2.histogram().plot(colorbar={"type": "log"})
こちらは death (Y軸) が 0.0125 より大きいあたりにぱらぱらと birth-death pair が分布しているのが特徴的です．
数値データの読み出し¶
pd1 や pd2 が指すオブジェクトの births、deaths属性を調べることで、birth time、death timeがわかります。
pd1.births
array([0.00140906, 0.00139591, 0.00134116, ..., 0.01572219, 0.01709659,
0.01871588])
pd1.deaths
array([0.0015926 , 0.00164399, 0.00170775, ..., 0.0157662 , 0.01717465,
0.01880101])
そこで、この2つの差を見ることでlifetimeが計算できます。
pd1.deaths - pd1.births
array([1.83534435e-04, 2.48078852e-04, 3.66588805e-04, ...,
4.40061409e-05, 7.80638251e-05, 8.51306753e-05])
lifetime のヒストグラムを表示してみましょう。
plt.hist(pd1.deaths - pd1.births, bins=100);
行末の ; としているのは plt.hist の返り値を無視するためのトリックです。大半の lifetime は非常に小さいことがわかります。実際対角線のそばに多くの birth-death pair がノイズ的な情報として分布していることはよくあります．
逆解析について¶
パーシステント図の個々の点は何らかの意味で元のポイントクラウドのリング構造、空隙構造と対応しているはずです。しかしそれがどのようなものであるのかを特定するのは実は そんなに簡単ではないです。このような解析を逆解析と呼びます。
ここでは HomCloud の強力な逆解析ツールを利用します．逆解析ツールには以下のような種類があります．
- Birth/Death simplices
- Optimal Volume
- Stable Volume
ここでは最新の機能である stable volumeを使います．これはoptimal volumeのノイズに弱いという問題を解決したバージョンです． (0.0025, 0.008) 付近にある birth-death pair の stable volume を調べます。
pd.nearest_pair_to で (0.0025, 0.008) に一番近い birth-death pair を検索することができます。
pair = pd1.nearest_pair_to(0.0025, 0.008)
このオブジェクトは Pair クラスのオブジェクトで、birth timeやdeath timeといった情報を保持しています。
pair
Pair(0.0025623095880009357, 0.008135892057712315)
pair.lifetime()
0.005573582469711379
以下のようにすると stable volume が計算できます。以下の 0.00005 は仮想的なノイズの大きさで，とりあえずは lifetime (death - birth) の1/10から1/100にしておけばよいでしょう．
stable_volume = pair.stable_volume(0.00005)
boundary_points メソッドで、対応するリング構造に含まれる点の座標が得られます。
stable_volume.boundary_points()
[[0.24041004740553085, 0.3620263927982651, 0.3938519814000714], [0.07850470821281752, 0.31832538225761675, 0.2726051865809148], [0.1255383953826733, 0.0800900311964785, 0.7190957020829821], [0.1252375238953729, 0.20843145021582987, 0.37381081780757186], [0.27896903483481006, 0.2900038108788685, 0.3853792732744701], [0.11968719444459341, 0.46213675229879714, 0.6086047255929676], [0.10439142042970573, 0.12004955606294554, 0.3999294686167837], [0.07478379187666995, 0.1318144315592794, 0.6167927456566142], [0.241996106473225, 0.4429189262369284, 0.4639170406136188], [0.12423094383664512, 0.3622394365995112, 0.6448082172747804], [0.19443369660602383, 0.2643008696498902, 0.7685550494906768], [0.41898602615433533, 0.44362916692289767, 0.3710002303374377], [0.12195279248515212, 0.003239458152972219, 0.6061209669659768], [0.21608561791517278, 0.2918069725141198, 0.3219258262415402], [0.1894939883612946, 0.03095999913576697, 0.6762565272706147], [0.0708147888171643, 0.05566245889432686, 0.6142169362499716], [0.39171929078549805, 0.4405548898038244, 0.288435385498083], [0.21062788160417378, 0.11633529728096403, 0.5162505592185838], [0.3166872139448015, 0.38348372951946463, 0.33415602643779374], [0.3806980910779977, 0.4089441782551778, 0.43539259723846135], [0.17739556404702383, 0.10003158291956527, 0.43755332223623955], [0.1563951908464587, 0.13629542421604657, 0.594303189697284], [0.15814254898557367, 0.44579878013749064, 0.4799628611505681], [0.17887993848973416, 0.42554668220768377, 0.6217943706156428], [0.09845847975583133, 0.26404248130005237, 0.7778474474038211], [0.3373945662185728, 0.46415106121781036, 0.4856613355037861], [0.08346167978435703, 0.26153343284444097, 0.3241366037151565], [0.08561651425017891, 0.42297356026275923, 0.528205350556188], [0.12886238414379725, 0.17512618876757002, 0.7438074952407614], [0.16660019888277078, 0.33716865816694763, 0.30111066188327684], [0.32035651808142795, 0.4751033316678963, 0.34029734006837487], [0.18678772331743787, 0.34044366488617717, 0.7226556446102448]]
このリング構造は39点からなっていることがわかります。boundaryメソッドを使うとどの点とどの点がつながっているか等もわかります。
このstable volumeを3次元可視化してみましょう。
pl = pv.Plotter()
pl.add_mesh(stable_volume.to_pyvista_boundary_mesh())
pl.show()
Widget(value="<iframe src='http://localhost:35823/index.html?ui=P_0x7f948d947220_1&reconnect=auto' style='widt…
リングが表示されます。
pyvistaを使ってポイントクラウドと重ねて表示しましょう．pyvistaの機能を使って線の太さや色を調整します．
pl = pv.Plotter()
pl.add_mesh(pv.PointSet(pointcloud))
pl.add_mesh(stable_volume.to_pyvista_boundary_mesh(), color="red", line_width=4)
pl.show()
Widget(value="<iframe src='http://localhost:35823/index.html?ui=P_0x7f948d858040_2&reconnect=auto' style='widt…
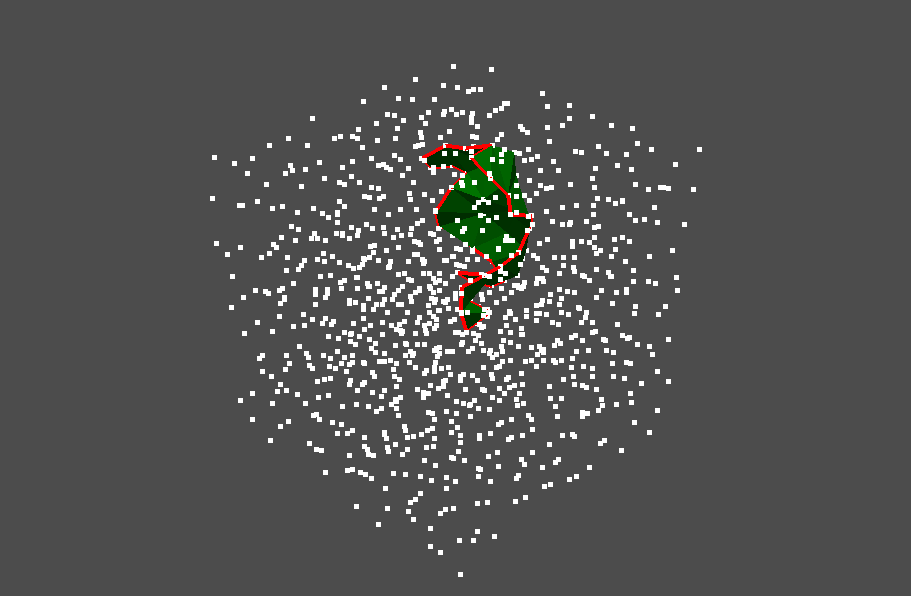
以下のように可視化されます．3次元データを回転させて見てみましょう．
stable volumeの中身 (ループが囲っている領域)の可視化もできます．
pl = pv.Plotter()
pl.add_mesh(pv.PointSet(pointcloud))
pl.add_mesh(stable_volume.to_pyvista_boundary_mesh(), color="red", line_width=4)
pl.add_mesh(stable_volume.to_pyvista_volume_mesh(), color="green")
pl.show()
Widget(value="<iframe src='http://localhost:35823/index.html?ui=P_0x7f948d7c2d10_3&reconnect=auto' style='widt…
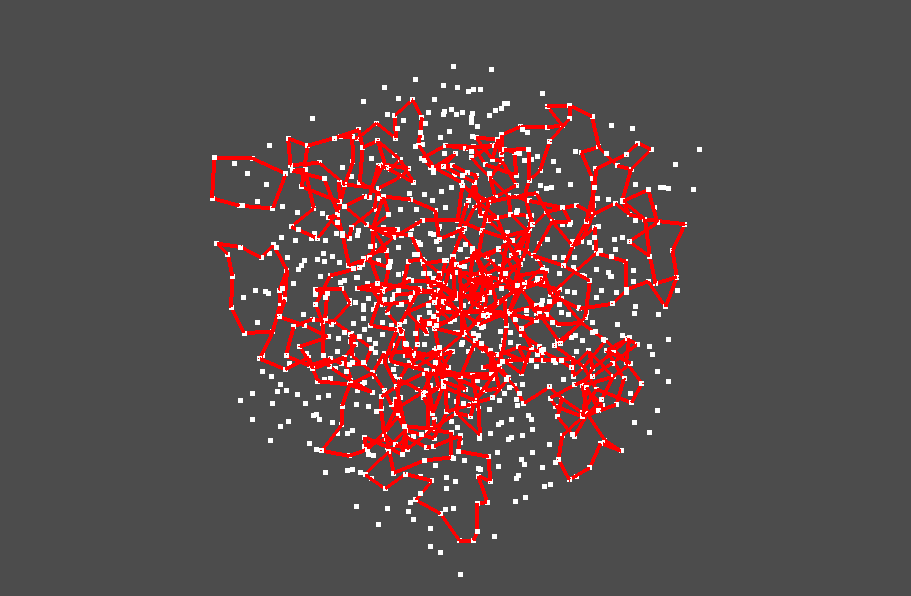
こんどは複数の点のstable volumeを同時に可視化してみます．birth < 0.004, death > 0.006 くらいの領域の birth-death pair を 以下のようにして取り出してきます．
pairs = [pair for pair in pd1.pairs() if pair.birth_time() < 0.004 and pair.death_time() > 0.006]
取り出してきた birth-death pair は以下のようにして数えることができます．
len(pairs)
54
では stable volume を計算して，可視化してみましょう．54個もあるので計算には結構時間がかかります．そこで
cutoff_radiusというのを指定します．これは計算ターゲットが存在する領域の大きさを指定することで計算時間を
削減するための仕組みです．だいたいこの球の内側にあるだろう，という領域の半径を指定します．
この半径を予想するのは簡単ではありませんがここではデータ全体の座標が0〜1の間なので適当にその半分の
0.5くらいでいいかな，と予想してやりましょう．
%%time
stable_volumes = [pair.stable_volume(0.00005, cutoff_radius=0.5) for pair in pairs]
CPU times: user 9.45 s, sys: 161 ms, total: 9.61 s Wall time: 11.3 s
pl = pv.Plotter()
for stable_volume in stable_volumes:
pl.add_mesh(stable_volume.to_pyvista_boundary_mesh(),
color="red", line_width=4)
pl.add_mesh(pv.PointSet(pointcloud))
pl.show()
Widget(value="<iframe src='http://localhost:35823/index.html?ui=P_0x7f948d862800_4&reconnect=auto' style='widt…
2次元のPDの逆解析について¶
空洞のほうも同様に可視化してみましょう．birth > 0.0125 かつ death - birth > 0.0005 などがおもしろそうです．
pairs = [pair for pair in pd2.pairs() if pair.birth_time() > 0.0125 and pair.lifetime() > 0.0005]
stable_volumes = [pair.stable_volume(0.000005) for pair in pairs]
pl = pv.Plotter()
for stable_volume in stable_volumes:
pl.add_mesh(stable_volume.to_pyvista_boundary_mesh(), color="green")
pl.add_mesh(pv.PointSet(pointcloud))
pl.show()
Widget(value="<iframe src='http://localhost:35823/index.html?ui=P_0x7f948d11a0e0_5&reconnect=auto' style='widt…
結構大きな空洞があるようです．
付録(発展的話題)¶
以下ではいくつか発展的な話題について紹介します．
頂点の命名¶
これまで boundary_points などで取り出せる頂点の情報は，XYZ座標のデータでした．これで不便のないことは多いでしょうが，「4番目の点」「12番目の炭素原子」のような情報を使いたい場合もあるでしょう．頂点に名前を付けることでこういった要望を実現することができます．
名前のルールとしては，文字列であればなんでもOKです．異なる頂点に同じ名前をつけることも可能です(HomCloud内部では同じ名前でも区別するので問題なく動作します)． ここでは1000個の点に"000", ... ,"999" という名前を付けましょう．
names = [f"{n:03d}" for n in range(1000)]
from_alpha_filtionのvertex_symbolsにこの名前のリストを渡すことで名前付けが可能になります．
hc.PDList.from_alpha_filtration(pointcloud, vertex_symbols=names, save_boundary_map=True, save_to="pointcloud-with-names.pdgm")
PDList(path=pointcloud-with-names.pdgm)
それでは上と同様stable volumeを取り出してその頂点を見てみましょう．boundary_pointsの代わりにboundary_points_symbolsを使うとループ上の点の名前のリストが得られます．
pd1 = hc.PDList("pointcloud-with-names.pdgm").dth_diagram(1)
pair = pd1.nearest_pair_to(0.0025, 0.008)
stable_volume = pair.stable_volume(0.0005)
stable_volume.boundary_points_symbols()
['392', '652', '147', '154', '297', '170', '442', '957', '832', '065', '580', '581', '582', '972', '080', '721', '480', '870', '872', '491', '236', '237', '750']
Optimal 1-cycle¶
Stable volume は内部的には線型計画法を用いて計算しています．点の個数が多い場合(100,000以上)は計算に時間がかかります．そこでHomCloudにはいくつか高速化のための仕組みがあります．
1DのPH，つまりループを解析する場合にはoptimal 1-cycleという道具を使って似たような情報を計算することができます．ただしこれはstable volume (やその元となったoptimal volume)とは異なる結果となってしまいます．普段はstable volumeのほうを使うことをお勧めしますが，点が多い場合にはこちらを使うことを検討してください．
以下，上の例と同様 (0.0025, 0.008) に一番近い点の optimal 1-cycle を計算します．
pair = pd1.nearest_pair_to(0.0025, 0.008)
optimal_1_cycle = pair.optimal_1_cycle()
可視化をします．
pl = pv.Plotter()
pl.add_mesh(optimal_1_cycle.to_pyvista_mesh(), color="red", line_width=4)
pl.add_mesh(pv.PointSet(pointcloud))
pl.show()
Widget(value="<iframe src='http://localhost:35823/index.html?ui=P_0x7f948da88b20_6&reconnect=auto' style='widt…
次のようにして，optimal 1-cycleに含まれる辺の情報を得ることができます．
optimal_1_cycle.path()
[[[0.1255383953826733, 0.0800900311964785, 0.7190957020829821], [0.1894939883612946, 0.03095999913576697, 0.6762565272706147]], [[0.1255383953826733, 0.0800900311964785, 0.7190957020829821], [0.12886238414379725, 0.17512618876757002, 0.7438074952407614]], [[0.12886238414379725, 0.17512618876757002, 0.7438074952407614], [0.09845847975583133, 0.26404248130005237, 0.7778474474038211]], [[0.19443369660602383, 0.2643008696498902, 0.7685550494906768], [0.09845847975583133, 0.26404248130005237, 0.7778474474038211]], [[0.19443369660602383, 0.2643008696498902, 0.7685550494906768], [0.18678772331743787, 0.34044366488617717, 0.7226556446102448]], [[0.18678772331743787, 0.34044366488617717, 0.7226556446102448], [0.2422121988843836, 0.4155487622456445, 0.7075748545403898]], [[0.3058423940248698, 0.3873355905611001, 0.6845908848342269], [0.2422121988843836, 0.4155487622456445, 0.7075748545403898]], [[0.3058423940248698, 0.3873355905611001, 0.6845908848342269], [0.3756708152548601, 0.4044688174747033, 0.6376955289875823]], [[0.42889440234947107, 0.4185878889153811, 0.5784790134722813], [0.3756708152548601, 0.4044688174747033, 0.6376955289875823]], [[0.42889440234947107, 0.4185878889153811, 0.5784790134722813], [0.4598816637670946, 0.4162817757882945, 0.49121522961841546]], [[0.47167872450123804, 0.3563222306553614, 0.4586659808644902], [0.4598816637670946, 0.4162817757882945, 0.49121522961841546]], [[0.47167872450123804, 0.3563222306553614, 0.4586659808644902], [0.4643529555106557, 0.38891409104439234, 0.37758039548286215]], [[0.41872842706632685, 0.3117355628197983, 0.36357591323139904], [0.4643529555106557, 0.38891409104439234, 0.37758039548286215]], [[0.41872842706632685, 0.3117355628197983, 0.36357591323139904], [0.39907517145005755, 0.2831943114569727, 0.4368217260059085]], [[0.34941504868714357, 0.20455144955416626, 0.4210171084082195], [0.39907517145005755, 0.2831943114569727, 0.4368217260059085]], [[0.34941504868714357, 0.20455144955416626, 0.4210171084082195], [0.296676557056482, 0.1310208804226647, 0.43046852751189457]], [[0.296676557056482, 0.1310208804226647, 0.43046852751189457], [0.2927591672470917, 0.11598883729155451, 0.5038453999131621]], [[0.21062788160417378, 0.11633529728096403, 0.5162505592185838], [0.2927591672470917, 0.11598883729155451, 0.5038453999131621]], [[0.21062788160417378, 0.11633529728096403, 0.5162505592185838], [0.1563951908464587, 0.13629542421604657, 0.594303189697284]], [[0.1563951908464587, 0.13629542421604657, 0.594303189697284], [0.07478379187666995, 0.1318144315592794, 0.6167927456566142]], [[0.0708147888171643, 0.05566245889432686, 0.6142169362499716], [0.07478379187666995, 0.1318144315592794, 0.6167927456566142]], [[0.0708147888171643, 0.05566245889432686, 0.6142169362499716], [0.12195279248515212, 0.003239458152972219, 0.6061209669659768]], [[0.1894939883612946, 0.03095999913576697, 0.6762565272706147], [0.12195279248515212, 0.003239458152972219, 0.6061209669659768]]]
PHTrees¶
2DのPH，つまり空隙を解析する場合にはPHTrees (persistence trees)が利用可能です．これは数学的な双対性を利用して2DのPHのデータを高速に計算する仕組みです．
まずはPHTreesを計算しましょう．次のようにsave_phtrees=Trueという引数を渡すことでPDの計算と一緒にPHTreesの計算をしてくれます．
hc.PDList.from_alpha_filtration(pointcloud,
save_to="pointcloud-phtrees.pdgm",
save_phtrees=True,
save_boundary_map=True)
PDList(path=pointcloud-phtrees.pdgm)
次のようにしてPHTreesを読み込みます．
phtrees = hc.PDList("pointcloud-phtrees.pdgm").dth_diagram(2).load_phtrees()
上のチュートリアルと同様，birth > 0.0125 かつ death - birth > 0.0005 というbirth-death pairに注目しましょう．PHTreesは内部的には木構造(厳密には複数の根を持つので森構造です)をしていて，各birth-death pairと木構造のノードが対応しています．
stable_volumes = [node.stable_volume(0.000005) for node in phtrees.all_nodes if node.birth_time() > 0.0125 and node.lifetime() > 0.0005]
次のように可視化します．
pl = pv.Plotter()
for sv in stable_volumes:
pl.add_mesh(sv.to_pyvista_mesh(), color="green")
pl.add_mesh(pv.PointSet(pointcloud))
pl.show()
Widget(value="<iframe src='http://localhost:35823/index.html?ui=P_0x7f948d11a530_7&reconnect=auto' style='widt…
形の情報は boundary_points メソッドや boundary メソッドなどで取り出せます．
stable_volumes[0].boundary_points()
[[0.6994453732085671, 0.13144153221118793, 0.5796928995428492], [0.601928672387627, 0.08671998624231247, 0.6583244074235682], [0.6994366874462885, 0.002942826575932589, 0.8357930347813906], [0.7794027918486173, 0.20026894822385644, 0.7191885213983096], [0.7064811805219977, 0.0026801020745949033, 0.5743802347904137], [0.8393149713230158, 0.04786549991547495, 0.6049694308550129], [0.8709165597839585, 0.12038179501110158, 0.6840309300141862]]
その他，PHTreesの木構造を利用した解析も可能です．詳しくはHomCloudのAPIマニュアルのPHTreesの項を見てください．
初期半径¶
粒子に固有の大きさがあるようなデータを解析したい場合，例えば複数種類の原子を含む原子配置データを解析したい場合，その半径を反映した解析が可能です．$i$番目の原子が$r_i$の半径を持つ場合，$w = [r_0^2, \ldots, r_{N-1}^2]$という配列を用意することでこの解析が可能となります．HomCloudのルールで半径は2乗する必要があります．
以下の例では1000個の粒子のうち最初500個の初期半径を0.01，残り500個の半径を0.05とします．
weights = np.concatenate([np.full(500, 0.01 ** 2), np.full(500, 0.05 ** 2)])
hc.PDList.from_alpha_filtration(pointcloud, weight=weights,
save_boundary_map=True, save_to="pointcloud-weights.pdgm")
PDList(path=pointcloud-weights.pdgm)
pd1 = hc.PDList("pointcloud-weights.pdgm").dth_diagram(1)
pd1.histogram().plot(colorbar={"type": "log"})
初期半径を正にすると，birthやdeathの値が負になる場合があります．これは球を初期半径から縮めている状況を考えています．
半径は$\sqrt{\alpha + r_i^2}$という方式で大きくしてきます($\alpha$を変化させる)．
BackgroundPlotter¶
pyvsita + jupyter notebook での可視化は時々性能不足の場合があります．
大きなボクセルデータの可視化の場合には特に表示されるまでの時間がかかる場合があります(これはおそらくバックエンド(python)とフロントエンド(ブラウザ+javascirpt)のやりとりで時間がかかっていると考えられます)．
また，jupyter notebookに埋め込まれているのが使い難い場合もあるでしょう．
そういう場合にはpyvistaqtのBackgroundPlotterを使うと良いです．
pyvsitaqtの利用にはpyqt6をインストールする必要があります．
BackendPlotter は普通の pyvista のPlotterとは共存できないことに注意してください． どちらか一方だけを使うようにするとよいでしょう．
import pyvistaqt as pvqt
pl = pvqt.BackgroundPlotter()
pl.add_mesh(pv.PointSet(pointcloud))
pl.show()